Imagico photo log
Does size matter? - On the issue of film and sensor formats
Cameras come with a large bandwidth of sizes of the light sensitive area - in the old days the film and currently in most cases the digital sensor. The number of opinions on the advantages and disadvantages of each of these form factors is even larger. A lot of these opinions are based on superficial observations and on a subjective personal like or dislike of a certain camera system. I want to shed some light on the basic physical background of this subject.
I want to keep this essay limited to the principal physical factors related to the choice of the form factor and i won't cover all the issues related to the actual camera systems available for each of those formats (although there will be examples in the text of course).
Film sizes and Sensor sizes
To just give some basic numbers at the beginning: The largest widely used film size was 8x10 inches which is about 20cm × 25cm. There were (and still are) even larger sizes of film but they are extremely rare in comparison. The smallest size was 8mm × 11mm used for example by the famous Minox cameras. A comprehensive list of film sizes can be found in the Wikipedia film format article.
With digital sensors the variety is somewhat smaller ranging from 6.1mm × 4.5mm in small compact cameras and cell phones (1/2.33 inch) up to about 56mm × 40mm in the largest medium format digital backs. This does not include scanning cameras of course.
Since aspect ratios of the different formats differs it is usually best for comparison to use the diagonal size of the sensor. This is also the size of the image circle the lens needs to produce to cover the full sensor or film.
Mechanics
The subject of mechanics essentially covers two aspects: Weight and precision. Assessing the weight of a camera in dependence of the sensor/film format is fairly simple. It scales with the volume of the camera which scales with the 3rd power of the linear size of the sensor. So given equal circumstances (same camera type and same materials) a 4/3 camera with a diagonal of about 21.5mm would be about 1/8 of the weight of a full format 24x36 camera (diagonal 43mm).
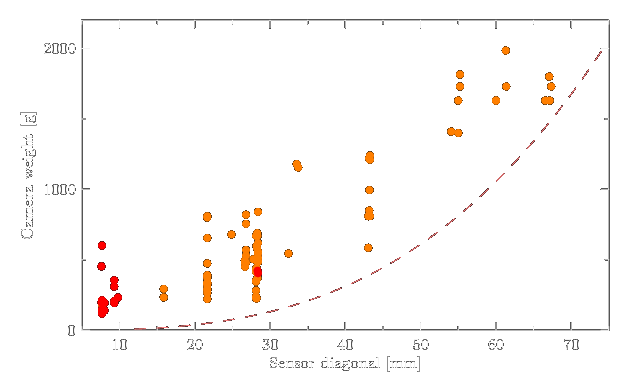
Does this also turn out to be the case with actual cameras available? Above is a diagram showing the weight of some currently available cameras in relation to their sensor sizes. The weights of the cameras with exchangeable lenses (orange dots) are just the plain cameras while the weight of the compact cameras with fixed lenses (red dots) of course include the lens. The dashed line shows a 3rd power of the sensor size function for comparison. As can be seen this marks the lower limit of existing cameras quite well. You also have to keep in mind that there is of course some offset due to ergonomics – even a camera with a very small sensor will have a certain minimum size so it can still be handled comfortably. In other words: a lot of the smaller cameras weight more than they would need to from the physical perspective since they feature a grip, a reasonably sized shutter release and a comfortable display.
So in summary if you want a lightweight camera you need to choose one with a small sensor. This however is only valid up to the point where ergonomics limit a further reduction of weight. In case of compact cameras the sensor size is usually not the defining factor for the weight of the camera.
The second aspect of mechanics that needs to be considered is precision. In simple terms: a small sensor camera needs to have tighter tolerances in its mechanics to produce the same quality of images as a larger sensor camera. What consequences does this have? On the bright the tolerances of manufacturing techniques also scale with the size of the workpiece. Example: producing a 10m steel girder with a tolerance of just 1mm is pretty hard while this is no issue for a 5cm bolt.
With actual cameras the situation is not so simple though. To be able to guarantee tighter tolerances with smaller camera components you would need to use different machining and assembly techniques. This is rarely the case however, especially with interchangeable lens cameras. The machining techniques used to produce the lens mount or the focussing gears of a 4/3 camera are not much different from those used in medium format for example. The situation is similar for lenses. While large diameter glass like that of fast long telephoto lenses is difficult to produce in high quality and specialty glass like molded asphericals can be created in much higher precision when size is small for most types of glass the achievable quality does not differ much across the range of sizes commonly used for photographic lenses.
Light sensitivity
Let's make a little thought experiment and imagine shrinking a larger camera (including its optics) to produce a smaller but otherwise identical one. It should be immediately obvious that the small camera will collect less light when taking a photo than the larger one. Does this affect the quality of images taken with this camera?
It does. The reason is that light – as you might already know – comes in discrete packages called photons. These photons pass through the lens and reach the sensor where they generate an electrical signal that is digitally recorded and stored by the camera. The problem with shrinking a camera is that you cannot divide a photon. If you for example have a full frame 24x36mm camera and a 50mm f/1.4 lens wide open. Let us say at certain settings a certain pixel of that camera receives 2 photons during an exposure. Now for comparison imagine a 4/3 camera with a 25mm f/1.4 lens - that would be close to a shrinked version of the first camera. This second camera would record only about 1/4 of the light of the first camera since the lens opening has only 1/4 the area and the camera has about the same angle of view. So depending on chance the same pixel in the image would receive either one or no photon. As a result there would be more noise [1].
You might suggest simply using a longer exposure on the smaller camera to work around this. And indeed this is done to some extent. You might notice that a lot of compact cameras with small sensors offer a much lower base sensitivity than DSLRs. This simply means that at base sensitivity and using the same aperture they require a longer exposure time.
There is another side to this problem though and this has to do with the way digital image sensors record light. During exposure the light incident to a sensor pixel generates an electrical charge which, after the image is taken, is read out and converted into digital numbers. There is a maximum amount of light (or number of photons) that can be recorded by each pixel before it spills over like a bucket filled with water. And that maximum amount is larger for large pixels. So a smaller sensor will not only receive fewer photons, it will also saturate earlier when it receives a lot of them. This limits the dynamic range, the ratio of maximum and minimum light levels that can be reliably recorded by the sensor. In other words: the above mentioned technique to use longer exposure times to compensate for the reduced amount of light available to small sensor cameras is soon limited by saturation of the sensor in the brighter parts of an image.
So much for the physics which are strongly in favor of a larger sensor – there is an aspect working for the smaller one though. Smaller sensors are much easier to manufacture than larger ones. This means small sensors also tend to be technologically more advanced and more efficient than larger ones. In terms of noise (i.e. the signal recorded even if there is no light at all) and basic efficiency (i.e. how reliably a photon is detected by the sensor) smaller sensors surpass the larger ones and this makes up for some of the disadvantages due to basic physics [1] [2] [3].
Depth of field
Depth of field (DOF) is often used as an argument for or against a certain sensor size – sometimes with proper arguments but often not. I will try to shed some light on this matter here.
DOF in the most general form refers to the way subjects in a photograph that are farer or nearer than the focus distance are rendered in varying degrees of sharpness or blurriness. DOF as a quantity refers to the range of distances around the actual focus distance that are still considered in focus. Since the transit from in focus to out of focus is gradual specifying a DOF requires defining a so called circle of confusion which is nothing more than a threshold of how much blur in the image that is still considered to be in focus.
Calculating the DOF as a function of the various properties and settings of a camera system is fairly complicated. To simplify discussion i will only talk about the hyperfocal distance here. The hyperfocal distance is the focus distance that needs to be set for the DOF reaching up to infinity. A small hyperfocal distance means a large range of distances can be kept in focus at the same time so there is a large DOF. This is strongly simplified of course but quite sufficient to consider the influence of the sensor size).
For calculating the hyperfocal distance H from a known circle of confusion c, the focal length f and the f-number N there is a simple and widely known formula [4]:
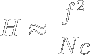
If we now refer to the previously used thought experiment and shrink a larger camera including both optics and sensor N stays the same while f and c scale according to the shrinking factor (for the focal length this is obvious but of course we also have to reduce the circle of confusion to obtain comparable results on a smaller sensor with smaller pixels). Using the same example as previously (24x36mm sensor and 50mm f/1.4 lens vs. 4/3 sensor with 25mm f/1.4 lens) and a circle of confusion of 0.03mm and 0.015mm respectively we can calculate a hyperfocal distance of 60m (for the 24x36mm camera) and 30m (for the 4/3 camera). So the 24x36mm sensor camera has a much smaller DOF or in other words: the 4/3 camera would need a lens 2 stops faster to obtain a similarly shallow DOF [5] [6].
We can also have a look at the matter of DOF from a somewhat different side. Since N = f/D (with D being the size of the entrance pupil, in case of long focal length lenses that is roughly the same as the front diameter of the lens) we can reformulate the above equation to
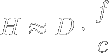
Since f/c is constant when shrinking a camera while keeping the angle of view and the number of pixels the same the hyperfocal distance will only depend on D. So when comparing different cameras you can say the larger the entrance pupil the smaller the DOF (in fact this rule can also be used when comparing different viewing angles at the same magnification) [7].
Resolution
You might have noticed resolution already turned up when we discussed DOF in form of the circle of confusion. Resolution in digital photography is often only associated with the number of pixels of the image sensor (i.e. the megapixel count). This is wrong for the most part though. The number of pixels of a sensor defines an upper limit for the resolution of a photograph. With current cameras this is often not what limits actual resolution of photographs though [8].
But i do not want to discuss resolution in general here, instead i want to see what influence the sensor size has on this subject. So apart from the number of pixels we also ignore the obvious requirements of precise focussing and steady holding of the camera here although these are often essential when operating near the resolution limit of current cameras. What remains are two influences, namely the quality of the optical system and diffraction.
Diffraction is a natural effect that influences light near the edges of an optical system – in this case the camera lens. In simple terms light near the edge of a lens does not follow the rules of ray optics and therefore this light reduces contrast and thereby reduces resolution. This is a hard physical fact and nothing can be done to prevent it. Since diffraction happens at the edges of the optical system it is of higher importance if the diameter of the lens is small or the lens is stopped down (i.e. artificially reduced in diameter by closing the aperture). The effect of diffraction only depends on the f-number. Two lenses at the same f-number, no matter what focal length, introduce the same amount of blur due to diffraction.
Since the number of pixels of the sensor define an upper limit for the resolution we can determine the f-number where the effects of diffraction exceed this limit. For f-numbers equal to or higher than this limit (i.e. smaller apertures) the resolution of the sensor will no more be the defining factor for the resolution of the camera as a whole. There are various tools available for calculating the diffraction limit [9]. Below is a table showing the diffraction limit for a 12 Megapixel camera at various common sensor sizes:
| Sensor size | Diffraction limit |
|---|---|
| 24x36mm | f/16 |
| 16x24mm (APS-C) | f/11 |
| 13x17.3mm (4/3) | f/8 |
| 8.8x13.2mm (Nikon 1) | f/5.6 |
| 1/1.6 inch | f/4 |
| 1/2.33 inch | f/2.8 |
Please note that these limits do not mean that for larger apertures you will not see any influence of diffraction on the result. It just means at the given aperture a further increase in the number of pixels of the sensor would no more increase the resolution of the resulting image, even under the best circumstances.
From this we could deduce that we should always use a large aperture lens wide open to minimize the effect of diffraction. This is only one side of the medal though – the other is the quality of the lens. All photographic lenses produce optical aberrations to some extend. These not only result from flaws and inaccuracies during production but are there by design. And these aberrations tend to be more significant for large apertures. Stopping down a lens tends to reduce aberrations.
So when trying to get the best resolution of a camera one would need to avoid large apertures due to optical aberrations and small apertures due to diffraction. There is a sweet spot for every camera lens combination. This sweet spot is rarely at the largest aperture [10]. For high quality medium aperture lenses it can be reached a single stop down from the widest aperture while for lower quality lenses you will often need to stop down 2-3 stops to get best results [11] [12].
Now what does this have to do with sensor sizes? As you can see from the table above you will need larger apertures (smaller f-numbers) to avoid the effects of diffraction with small sensors. And indeed many better compact cameras have zoom lenses with maximum apertures f/2 or faster while most standard zoom lenses for 24x36mm are f/2.8 or slower. But it is quite hard to design a f/2 zoom lens with few optical aberrations wide open or at f/2.8, even for the small image circle of a small sensor.
Giving an example again: there are quite a few lenses for the 24x36 format where the sweet spot with currently available cameras is already at f/5.6 or wider, i.e. at least three stops from the diffraction limit with 12 MP. A comparable lens in terms of resolution for a 1/1.6 inch sensor (like it is built into high end compact cameras) would need to reach best quality by f/1.4. To my knowledge no such lens exists.
So summing things up for resolution a larger sensor is favorable as well since you will be less limited by diffraction compared to a similar camera with a smaller sensor and counteracting this problem by using large aperture lenses will lead to more problems with optical aberrations
Conclusions
The subject of this essay was how the size of the film or image sensor in a camera affects the quality of the photographic results. I have discussed various aspects that needs to be considered and these are the most important conclusions:
- With a larger sensor a camera will be larger and heavier. In case of very small sensors (4/3 and smaller) the sensor size is no more the defining factor for the camera size and weight though due to ergonomics.
- A larger sensor a camera will allow for better image quality when all other things are equal. Due to the technical difficulties of producing large sensors 'other things' are not equal though and the advantage of large sensors is sometimes smaller than one would expect in reality.
- Small sensors will result in a larger DOF with similar lenses (same angle of view and f-number). This means in practical application it will be more difficult to create photos with a shallow DOF with small sensor cameras. It is not easier to obtain a larger DOF with a small sensor camera due to diffraction though.
- Creating a high resolution photograph with a small sensor camera requires higher quality lenses than with a larger sensor camera. Such lenses are difficult to design and manufacture so cameras with small high resolution sensors often have no lenses matching this resolution.
Further reading
A lot has been written on the various aspects discussed above already. A selection of sources is given below. Please note though the subject of sensor sizes is quite controversial. There are many advocates for certain sizes or brands making use of these sensor formats who sometimes have a strong bias in their writing. Therefore you should maintain a critical attitude when reading anything on the matter.
Kommentare:
habe ich richtig gelesen? Das am weitesten verbreitete analoge Filmformat soll 20cm x 25cm gewesen sein? Waren es nicht doch vielleicht Millimeter?
Gruß
Groß
nicht das am weitesten verbreitete, sondern das größte verbreitet genutzte Format.
Durch das Abschicken Ihres Kommentars stimmen Sie der Datenschutzrichtlinie zu und erlauben, dass die eingegebenen Informationen (mit Ausnahme der eMail-Adresse) in diesem Blog veröffentlicht werden.